Julia Set Generator

Roland Braune

February 26th, 2003

The Julia Set Generator is a .NET Windows Forms application for generating images of Julia Sets of quadratic and also higher order. The transformation which determines a Julia Set can be changed within the application. The specified expression is parsed by the program and dynamically transformed into MSIL Byte Code using the Reflection.Emit framework. This ensures good performance also for complicated expressions (e.g. polynomials of a higher degree). The application is written in C#.

Introduction

Julia Sets are subsets of the set of complex numbers. A Julia Set is set that is invariant with respect to a particular transformation on the complex plane. These transformation are usually given by parametrised rational polynomial expressions e.g. f(z) = z⁴ + z³/(z+1) + L where L is a complex number representing the parameter Lambda.

This transformation is used to define a dynamical system {X,f} where X is a metric space (the complex plane in out case). In a dynamical system the transformation f is applied iteratively to a point x in X. The resulting sequence of points is called the orbit of the point.

A Julia Set is therefore a set of points whose orbits consist solely of points from the set itself. So each chained application f(f(f(...(f(z))...) of the transformation reaches a point in the set. A filled Julia Set is a Julia Set merged with the set of points whose orbits converge to the origin. All other points outside the Julia Set converge to infinity.

Let us consider the "classic" Julia Set defined by the transformation f(z)=z²-L where L=1.1. The set of black points is the filled Julia Set. The boundary of this filled Julia Set is the Julia Set for the given transformation.

This image was computed using the so called "Escape Time Algorithm". This algorithm takes a clipping area of the complex plane and computes the orbit of each point in this area. If the orbit exceeds a certain threshold (also called escape radius) before a specified number of iterations is reached, the point is considered not to belong to the (filled) Julia Set. If the orbit does not exceed the escape region (that is when it wanders around or converges to the origin), it is assumed to belong to the filled Julia Set and a corresponding pixel is set on the screen.

Julia Sets can be classified as fractals. On the one hand they have a fractional (nonintegral) dimension (fractal dimension) greater than their topological one. On the other hand they often exhibit self-similarity. Selected fragments appear in a smaller scale on various other locations of the image or parts of the image seem to be minimized copies of the image as a whole.

The following web page offers a good source for further and more detailed information on Julia Sets: http://www.mcgoodwin.net/julia/juliajewels.html

Using the application

Entering the data

In the main application window click Edit Data on the Julia Set menu.
A dialog box displays in which you can enter the data that will be used for computing the Julia Set image.

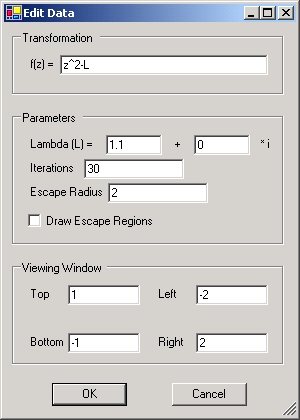
The following section gives a brief description of each field:

Transformation (f(z))
The complex transformation used by the application in order to compute the image of the corresponding Julia Set. This transformation is usually given by a rational polynomial expression with a parameter Lambda (L) e.g. z²-L or z⁴-z-L.
Note: The only variable that is allowed to occur in the expression is z and the parameter Lambda is always denoted by the letter L. Besides that you cannot enter complex numbers directly as part of the expression. The only way to do this is using the parameter Lambda.
Lambda
The real and the imaginary part of the parameter Lambda used in the transformation expression.
Iterations
The maximum number of iterations for the Escape Time Algorithm. This is a very important parameter which has a great influence on the level of detail of the computed image. The higher the maximum number of iterations, the more detailed the image of the Julia Set will be.
Note: Specifying bigger numbers here requires more time to compute the image afterwards. The maximum number of iterations usually ranges between 20 and 1000.
Escape Radius
Defines a circle around the origin of the complex plane. It represents the threshold for the Escape Time Algorithm determining whether a point belongs to the filled julia set or not. If the orbit of a point exceeds this threshold it is certain that it will escape to infinity.
Draw Escape Regions
This flag tells the generator whether it should paint the escape regions or not. If this flag is true, the escape regions are painted alternately black and white depending on the escape time (odd or even).
Viewing Window
Defines the Top Left and Bottom Right corners of the clipping rectangle on the complex plane which the Escape Time algorithm should be executed on.

Starting the computing process

On the Computing menu in the main window, click Start.
A background thread is started to compute the image using the data from the dialog above.
The status bar of the main window shows the progress of the computing process as a percentage value. After the computing process has finshed, the new image is displayed on the screen.

Stopping the computing process

On the Computing menu in the main window, click Stop.
The background computing thread is stopped and the partially computed image of the Julia Set is displayed on the screen.

Zooming in

Press the left mouse button and leave it pressed while dragging the mouse to spawn a (red) zoom rectangle.
Release the left mouse button in order to start the computing of the image of the zoom area defined by the zoom rectangle.

Note: The maximum number of iterations does NOT increase when zooming into the image. Thus the level of detail decreases with higher zoom factors. This does not mean that the corresponding (mathematical) Julia Set also becomes less detailed when it gets magnified. This is only an effect of the Escape Time Algorithm, which can be (partially) avoided by either choosing a higher number of iterations or increasing the number of iterations depending on the zoom factor. The latter could be normally accomplished by the generator program but this functionality is not implemented in this version of the Julia Set Generator.

Zooming out

Click the right mouse button to restore the original non-zoomed image, defined by the data you have entered into the data dialog box last time.

Some interesting Julia Sets together with their parameters

*f(z)*	*L_Real*	*L_Imaginary*	Escape Radius	Max. Iterations	Draw Escape Regions
z²-L	1.1	0	2	30	-
z²-L	0.745	0.113	2	200	yes
z²-L	0.687	-0.312	2	100	no
z³+L	0.6	0.55	2	40	-
z³-L	0.5	0.5	2	30	-
z³-L	0.38453	0	2	100	-
z⁴-z-L	0.78	0	2	50	yes
z⁴+L	0.6	0.55	2	40	-
z⁵+L	0.8	0.6	2	60	-
z⁶-z²-L	0.525	0	2	100	yes

Installation

Download the file jsgen.exe, copy it to a folder of your choice and execute it.